Bayes

1. Karin

Ter introductie een probleem

Karin, 50 jaar, zonder symptomen, ondergaat een routinematig mammografieonderzoek. Ze test positief en is ongerust over de mogelijkheid van borstkanker en haar kansen. Karin wil van u weten of ze borstkanker heeft en wat haar kansen zijn.

De volgende gegevens zijn bekend

De prevalentie van borstkanker bij vrouwen van haar leeftijd is 1%.

True Positive (TP+): Hoe vaak is de test correct bij mensen met borstkanker? (90%)  

True Negative(TP-) : Hoe vaak is de test correct voor mensen zonder borstkanker? (91%)

In onderstaande tabel staat K+ voor het hebben van kanker, K- voor het niet hebben van kanker, T+ voor een positieve test(verdacht van kanker) en T- voor een negatieve test ( Niet verdacht van kanker)

Aan de kleur valt al te zien dat er bij deze procedure twee verschillende soorten fouten worden gemaakt. De persoon heeft borstkanker(K+) en de test is negatief (T-). De andere foutsoort is dat er geen kanker is (K-) en de test positief is (T+).

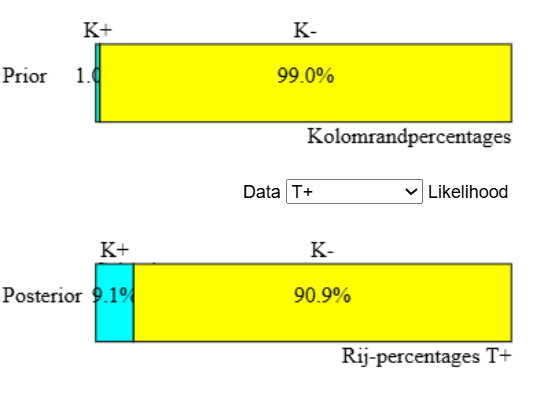
Voor Karin betekent dit dat haar kans dat ze kanker heeft van 1% naar 9,1% is gegaan.

Opgave: Controleer of de gegevens in de tabel kloppen met de gegeven percentages.

De psycholoog Gert Gigerenzer heeft dezelfde vraag gesteld aan een zaal vol oncologen. Hij gaf de vraag als een multiple choice vraag.

De kans dat Karin kanker heeft, is ongeveer

◯ 90%

◯ 80%

◯ 10%

◯ 1%

Maak je keuze!

Het bleek dat meer dan 50% van de oncologen voor 80% of 90% koos.

Opgave . Bereken de kans op borstkanker voor Karin als de uitslag negatief was geweest.

2. Reumatoide artritus

In 1. Karin, werd de tabel gegeven. In dit hoofdstuk moet jezelf eerst de tabel vullen. De eerste stap daarbij  is dat jezelf de bevolkingsomvang kiest, bijvoorbeeld 10.000

In de bevolking lijdt 1 op de 100 mensen aan reumatoïde artritis. Er bestaat een test, de "reumatest", die bij reumapatiënten meestal positief is en bij niet-reumapatiënten meestal negatief. De test is echter niet 100% waterdicht en heeft een specificiteit (dat wil zeggen de kans op een negatieve test als de ziekte afwezig is) van 0,8 en een sensitiviteit (kans op een positieve test bij aanwezigheid van de ziekte) van 0,7.

Vraag: Is het zinvol om de bevolking met deze test op het voorkomen van reuma te testen?

Daartoe bepalen we wat de kans is op de ziekte als we een willekeurig iemand uit de bevolking testen en de uitslag positief is.

Met Z geven we aan dat de testpersoon aan de ziekte lijdt en met + dat de uitslag van de test positief is. Uit de bovenstaande gegevens volgt:

P(Z)=0,01 (kans dat iemand de ziekte heeft)

P(T+|Z+)=0,70 (de kans op een positieve uitslag als de ziekte aanwezig is)

P(T-|Z-)=0,80 (de kans op een negatieve uitslag als de ziekte afwezig is)

Dit probleem wordt nu systematisch aangepakt. Eerst de tabel opschrijven met in de rechterbenedenhoek 10.000 als zijnde de omvang van de totale populatie. Gebruik de gegevens om  bij ?1 het totaal aantal zieken van de 10.000 in te vullen, dan is ook ?2 bekend, Vervolgens ?3, ?4 enzovoorts,

Opgave: Wat is de kans dat een testpersoon positief is en dat de persoon de ziekte heeft?

Opgave. Welke argumenten zouden een rol kunnen spelen of deze test zinvol is om landelijk te gaan afnemen?

3 Regel van Bayes

Thomas Bayes (1702 – 1761) was een Engels wiskundige en presbyteriaans predikant. De waarschijnlijkheidsrekening ontwikkelde zich in de 18e eeuw, onder andere door Jakob Bernoulli, Abraham de Moivre, Thomas Bayes en Pierre-Simon Laplace, die in 1812 zijn Theorie analytique des probabilites schreef. Meer geschiedenis van de kansrekening

De definitie van voorwaardelijke kans is.

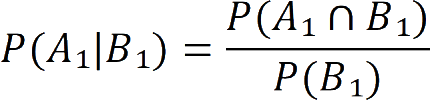
Opgave Controleer dat deze stelling klopt in de kruistabellen van paragraaf 1 en van paragraaf 2.

De aannemelijkheid gaat het beste met het mozaiek plot.

De oppervlakte van een vierkant linksboven is

en ook

Dit kun je in de mozaiek plot zien met behulp van de knop . Dus

Beide zijden delen door geeft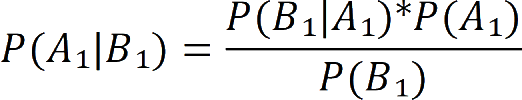

In de tabel kun je zien dat 2