Beslisbomen en random forest

Beslisbomen zijn een populaire en verrassend effectieve techniek. Hier zijn een aantal toepassingen van beslisbomen:

1.Medische Diagnoses: Beslisbomen worden vaak gebruikt om ziektes te diagnosticeren op basis van patiënteninformatie, zoals leeftijd, symptomen, en medische geschiedenis. Bijvoorbeeld, ze kunnen helpen bij het voorspellen van hart- en vaatziekten op basis van variabelen zoals bloeddruk, cholesterol en BMI.

2.Kredietwaardigheid: Financiële instellingen gebruiken beslisbomen om te beoordelen of een lening aan een klant kan worden verleend, door factoren zoals inkomen, kredietgeschiedenis en werkstatus in overweging te nemen.

3.Klantenclassificatie: In de detailhandel worden beslisbomen gebruikt om klantsegmentatie uit te voeren. Dit helpt bedrijven te begrijpen welke klanten waarschijnlijk bepaalde producten zullen kopen op basis van hun demografische gegevens en aankoopgeschiedenis.

4.Fraudedetectie: Banken en verzekeringsmaatschappijen gebruiken beslisbomen om verdachte transacties te identificeren door verschillende kenmerken van transacties te analyseren, zoals het bedrag, de frequentie en de locatie.

5.Marketingcampagnes: Beslisbomen kunnen helpen bij het voorspellen van de effectiviteit van marketingcampagnes door te analyseren welke groepen consumenten waarschijnlijk op bepaalde aanbiedingen zullen reageren.

6.Energiebeheer: In de energie-industrie worden beslisbomen gebruikt om het energieverbruik te voorspellen en om te bepalen welke klanten het meest waarschijnlijk zijn om energiebesparende maatregelen te omarmen.

Elke toepassing demonstreert hoe beslisbomen kunnen helpen bij het nemen van geïnformeerde beslissingen door gegevens op een gestructureerde en begrijpelijke manier te analyseren. Dit maakt ze een waardevol hulpmiddel in een breed scala aan velden. Een enkele beslisboom is vaak te veel toegespitst op de data set waarmee getraind is. Een oplossing daarvoor is Random Forest. Met een neuraal netwerk kan dit probleem ook worden aangepakt. Ook de oplosmethode met neurale netwerken kun je in deze app onderzoeken..

In deze app kun je onderzoeken hoe het algoritme werkt in de situatie van maar twee variabelen. De beperking van twee variabelen heeft het voordeel dat we het algoritme kunnen visualiseren. De taak is om gele driehoeken en blauwe vierkanten te scheiden met behulp van verticale en horizontale lijnen. Een kleine dataset maakt de uitleg makkelijker te volgen.

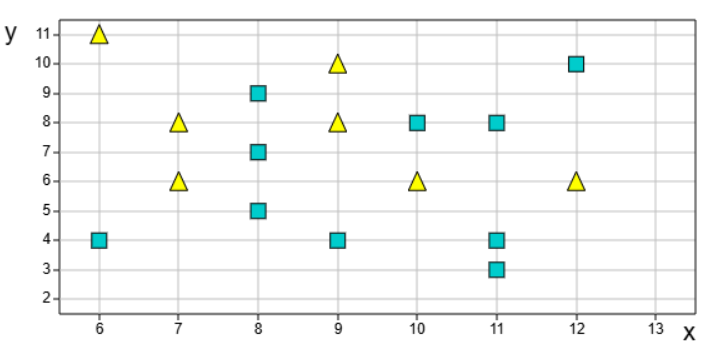
x is de horizontale as en y is de verticale as, Het algoritme geeft de volgende oplossing getekend als boom.

Een boom bestaat uit knooppunten en eindtakken. Bij de witte eindtakken wordt gekozen met de meerderheidsregel. Bij gelijke aantallen wordt gedobbeld.

Hieronder staat de oplossing getekend met horizontale en verticale lijnen. Je kunt gemakkelijk nagaan dat het dezelfde oplossing is als met de boom.

Nu nogmaals de procedure maar nu met meer aandacht voor de details. Voor de uitleg gebruiken we de kleine dataset

Als je de app opent, verschijnen er vier rechthoeken op je scherm. Behalve bij de eerste rechthoek kun je bij de overigen het aantal elementen in de dataset aanpassen. De datasets zijn iedere keer als je opstart weer anders, net zoals ook in de echte wereld. Het toeval speelt steeds een rol. Je start het proces door op een van deze rechthoeken te klikken. Dit is dan de dataset waarmee de app begint. Je kunt deze dataset aanpassen door figuren toe te voegen, te verwijderen of te slepen. Je kunt ook van vierkant naar driehoek en vice versa(Toggle) . Als je in je les gebruik wilt maken van zo'n dataset, kun je een geschikte dataset downloaden en later in de les weer uploaden. Deze dataset kan je ook in de app Data analyse gebruiken.

Deze app kent twee methoden (Minimum aantal fouten en Gini). Er zijn nog meer methodes zoals bijvoorbeeld Entropie

Bijvoorbeeld bij het volgende eindblad worden bij welke keuze dan ook drie of meer fouten gemaakt.

Iedere keer als er weer een beslissing moet worden genomen, kiest het algoritme de keuze met het minste aantal fouten. Als het minimum aantal fouten 0 is, kan het resultaat niet meer verbeterd worden.

Het minimum aantal fouten van een parent is de som van het minimum aantal fouten van zijn takken., In het figuur hieronder dus 0+4=4

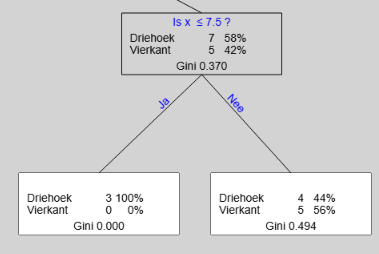
Deze methode leidt vaak tot betere resultaten. Ook deze methode streeft naar een zo klein mogelijk getal. Ook bij Gini is geen verdere verbetering mogelijk als de gini-index 0 is.

Gini is een maat voor ongelijkheid

Aantal geel	4
Aantal blauw	5

Als je 4 gele ballen en 5 blauwe ballen hebt in een vaas, dan is de kans dat je twee verschillende kleuren trekt 1 min de kans dat je twee gelijke kleuren trekt. Je trekt met teruglegging.

Op de pagina Data aanpassen is de knop

Daar kun je de gini-berekeningen laten uitvoeren.

De Gini-index van de parent is het gewogen gemiddelde van de twee children. In de boom hierboven is dat (3/12)*0+(9/12)*0,494=0.370

Deze parameter bepaalt de maximale diepte van de boom. Hoe dieper de boom, hoe complexer het model. Een diepere boom kan beter passen bij de trainingsgegevens, maar het kan ook leiden tot overfitting. Om overfitting te voorkomen, kunnen we de diepte van de boom beperken door een maximumwaarde in te stellen voor maximale diepte

Je krijgt onderstaande plaatje door op de knop

te klikken.en de maximale diepte op 0 te zetten. Het rode getallenpaar (7,10) geeft aan 7 gele driehoeken en 10 blauwe vierkanten.

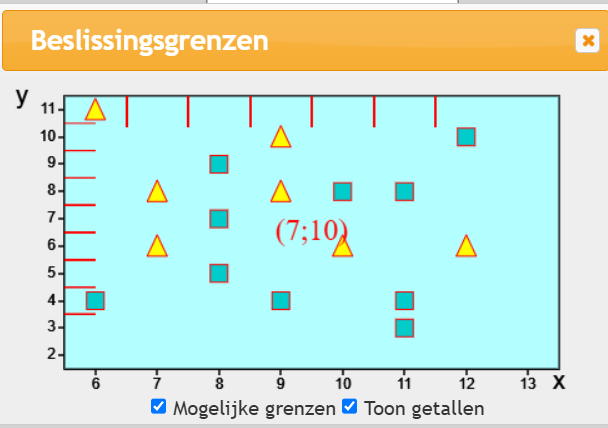
Het algoritme laat zich het beste uitleggen met behulp van bovenstaande plaatje. De rode streepjes zijn alle punten die onderzocht moeten worden als mogelijke grenslijn.. De rode streepjes staan precies tussen de data-punten. Degene die het beste resultaat geeft, wordt genomen

Als eenmaal de beslissing is genomen (y=5,5), moet vervolgens de twee rechthoeken die zijn ontstaan, apart onderzocht worden. De onderste rechthoek, bevat 5 vierhoeken en kan dus niet meer verbeterd worden.

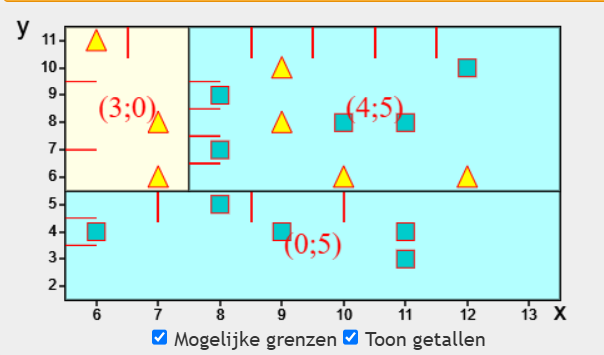
De bovenste rechthoek kan kennelijk ook nog verbeterd worden (x=7,5),.Dit splitsen gaat door totdat de maximale diepte van de boom bereikt is, of als er geen verbeteringen meer mogelijk zijn.

Bij iedere variabele horen een aantal beslispunten. Beslispunten liggen tussen twee opeenvolgende waarden die aangenomen kunnen worden. Iedere laag opnieuw onderzoekt de mogelijke verbetering van alle variabelen naar alle beslispunten van die variabele en kijkt dan welke keuze op dat moment de grootste verbetering geeft. Dit is een greedy algoritme. Dat wil zeggen dat het algoritme maar één stap verder kijkt. Je kunt het ook zien met de app als je de maximale diepte van de boom kleiner of groter maakt, dan verandert er niets aan de rijen erboven.

Een knooppunt waar minder dan het aantal opgegeven records doorheen gaan, wordt niet verder gesplitst. Dit om overfitting te voorkomen.

Op de knooppunten wordt de verhouding tussen de twee groepen weergegeven met een smalle horizontale balk. Zo zie je in een opslag de keuzes. In kleuren taal: Probeer de rechthoeken zo geel of zo blauw als mogelijk te maken

Soms is er sprake van overbodige vragen. Bijvoorbeeld als beide childs hetzelfde antwoord geven vanwege de meerderheidsregel. Als de berekeningen zijn gedaan, wordt nog een keer door de boom heengelopen om overtollige takken weg te snijden. Je kunt het gemakkelijkste het effect van prunen zien in het plaatje van de beslissingsgrenzen als twee rechthoeken naast elkaar dezelfde kleur hebben, dan worden die bij het prunen bijelkaar gevoegd..

Een verwarringmatrix is een tabel die gebruikt wordt om de prestaties van een classificatiemodel te evalueren. Het toont het aantal juiste en aantal onjuiste voorspellingen van het model voor elke klasse in de dataset. De kolommen geven de voorspelde labels weer, terwijl de rijen de ware labels weergeven. De hoofddiagonaal van de matrix geeft het aantal correcte voorspellingen weer (true positives en true negatives), terwijl de off-diagonale elementen het aantal incorrecte voorspellingen weergeven (false positives en false negatives). Een verwarringmatrix geeft een gedetailleerd beeld van de prestaties van het model, waardoor metrieken zoals nauwkeurigheid, precisie, recall en F1-score kunnen worden berekend, die kunnen worden gebruikt om de kwaliteit van het model te beoordelen en gebieden voor verbetering te identificeren,

Eerst moet je de grootte van de test set opgeven. Pas als je de opdracht hebt gegeven om de testlijst opnieuw te trekken wordt de testlijst echt getrokken. Om een beslissingsboommodel te bouwen, moet je eerst je gegevens opsplitsen in een trainingsset en een testset. Vervolgens gebruik je de trainingsset om het model te bouwen en de testset om de prestaties te evalueren.

De nummers uit de testlijst verschijnen onder de tabel. De groen gekleurden zijn goed voorspeld en de rood gekleurden zijn verkeerd voorspeld Door erop te klikken wordt het pad door de boom getoond en ook rechtsboven de waarden van de variabelen van dit record.

Random forest

Beslisbomen suggereren vaak een veel preciezere oplossing als wenselijk is. Vaak is er, speciaal als het om veel variabelen gaat, sprake van overfitting. Overfitting treedt op wanneer een algoritme te nauw aansluit bij de trainingsgegevens, wat resulteert in een model dat geen nauwkeurige voorspellingen doet of conclusies kan trekken.

Het basisidee bij random forest om veel bomen aan te maken op grond van iets gewijzigde gegevens. Wat betreft de data maakt men gebruik van de bootstrap. en van het kiezen van een selectie van de variabelen. In deze app wordt alleen gebruik gemaakt van de bootstrap.

Dit is een van de veertig bomen die aangemaakt zijn. In de gekleurde rechthoeken staan driehoeken en vierkanten met een dikke rand en zelfs ook zonder rand. De figuren zonder rand zijn niet uitgekozen. De figuren met rand zijn wel gekozen. Des te dikker de rand des te vaker zijn ze gekozen. Dit is de bootstrap methode. Uit de hele trainings-data-collectie wordt steeds records getrokken. Bij deze handelswijze wordt ongeveer een derde van de trainingset niet getrokken. Deze groep ( Out Of Bag) doet deze keer dus niet mee met de berekeningen van de boom en kan dus ook gebruikt worden hoe goed de boom de uitkomst voorspelt. In boven staande wordt er dus 2 records verkeerd ingedeeld..

Om de knop random forest

uit te leggen maken we gebruik van een veel grotere dataset. De vierde rechthoek met 610 records De omvang van de testset is 115. Deze is random getrokken uit de populatie.

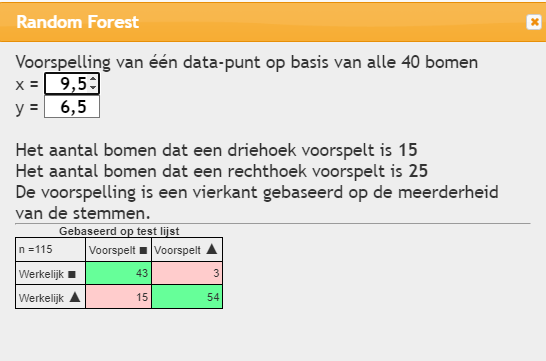
Random Forest voorspelt voor ieder data-punt de verwachte waarde op grond van de 40 bomen die geconstrueerd zijn. De conclusie wordt getrokken met de meerderheid van de 40 bomen.

De kwaliteit van de random forest methode kun je beoordelen op wat het met de test-set doet. In bovenstaande geval is de accuraatheid 97/115=0,843.

Je kunt de voorspelling ook zien als je de optie

. Er verschijnt dat een cirkel op de grafiek met een oranje rand. Het midden van de cirkel is geel of blauw. Het getalletje dat er bij staat, geeft de kans op geel zoals bepaald door de forest methodel . Je kunt de cirkel met de muis verplaatsen,

Neurale netwerken

Werk eerst de app Neurale netwerken door. In de help bij Neurale netwerken staat uitleg en opdrachten. In de app Neurale netwerken ging het over het benaderen van een functie. Dat was een regressie probleem. De gemiddelde kwadratensom werd daar gebruikt als loss-functie.

Je kunt het probleem van voorspellen van gele driehoek of blauw vierkant ook aanpakken met een neuraal netwerk. De verliesfunctie is nu binary cross entropie. Een duidelijk verhaal op internet over deze methode staat hier

Zoals je ziet definieer je op dezelfde manier een neuraal netwerk. Geprobeerd is om het werken met het neurale netwerk zo gemakkelijk mogelijk te maken. Eerst leg je de hyper-parameters vast. Daarna start je de berekeningen. Je kunt steeds het aantal epochs verhogen. Ook tijdens de berekeningen. Ook kun je de uitvoering pauzeren om tussentijdse resultaten te bekijken. Pas als je de knop Opnieuw heb ingedrukt kun je het netwerk wijzigen en de hyper-parameters wijzigen. .

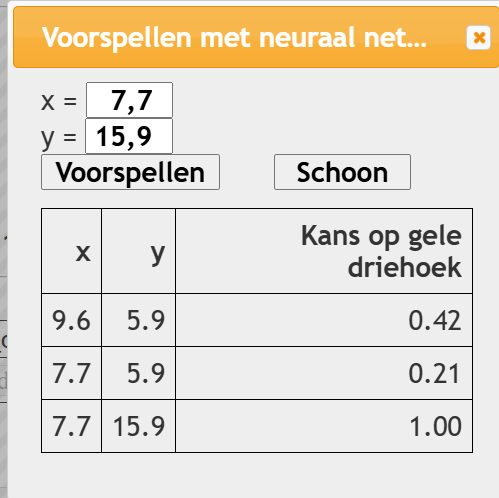
Je kunt bij het voorspellen ook om punten buiten de rechthoek vragen. Het programma geeft een antwoord, zonder te waarschuwen.

In de grafiek hierboven zijn de driehoeken en vierkanten getekend. In het midden staat de cursor. Het getal 0.59 is de kans op geel bij het punt van de muisaanwijzer

Deze loss grafiek geeft een beeld van een loss grafiek. De grafiek gaat meestal naar beneden, en stabiliseert min of meer met kleine schommelingen