De bedoeling van deze app is om met behulp van een neuraal netwerk een gedeelte van de parabool y=x² te benaderen met lijnstukken. In het eerste onderdeel met slechts één neuron, in het tweede onderdeel met twee neuronen en in het derde deel mag jezelf het aantal neuronen en lagen bepalen.
In de eerste twee onderdelen kun je zien wat er gebeurd. Je ziet de lijnen langzaam aan naar de grafiek verschuiven. In het derde deel krijg je alleen de resultaten te zien. Je kunt met de button 
links boven de app steeds opnieuw starten.
Netwerk met één neuron
De bedoeling is om met behulp van netwerk met slechts een neuron netwerk een gedeelte van de parabool y=x² te benaderen met een lijn.
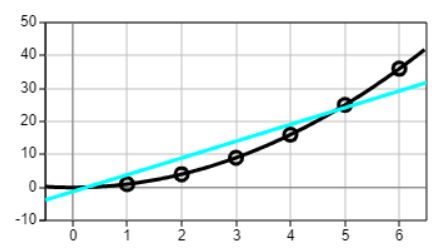
Met één neuron zijn er slechts twee knoppen waaraan je kunt draaien. De weight bepaalt de helling van de lijn en de bias de constante. Het is de bedoeling om dat de lijn zo dicht mogelijk langs 6 punten die op de parabool liggen, gaat. Het zijn de punten (1,1), (2,4), (3,9), (4,16), (5,25) en (6,36). Deze 6 punten zijn aangegeven in de grafiek hieronder. Natuurlijk is er geen lijn die exact door al deze 6 punten gaat. Wat een goede benadering is, is natuurlijk een keuze. In dit soort situaties wordt vaak de MeanSquaredError (gemiddelde kwadraten fout) genomen.. Hieronder zie je de grafiek van de parabool, de zes punten die we zo goed mogelijk willen benaderen en de tabel waarin de berekeningen staan voor de MeanSquaredError.
Draaien aan de knoppen
Met de knop Randomiseer worden steeds random-waarden tussen -10 en 10 gekozen voor de weight en voor de bias. Overduidelijk zijn er grote verschillen voor de MeanSquaredError.
Door te draaien aan de knoppen verandert ook steeds de meanSquaredError. Het is de bedoeling om de MeanSquaredError zo klein mogelijk te krijgen (0 zal niet lukken). Probeer maar eerst zelf om de MeanSquaredError kleiner te krijgen door te draaien aan de knoppen.
Met de knoppen bij Weight en bias kun je gemakkelijk het effect van een kleine verandering van een parameter onderzoeken.
Berekening MeanSquaredError
De berekening kun je zien in de tabel hierboven. In de eerste kolom staan de x-waarden en y-waarden van de parabool. In de derde kolom staat per rij het verschil tussen de echte y-waarde en de geschatte y-waarde. Deze kan zowel positief als negatief zijn. Door te kwadrateren krijg je alleen maar positieve getallen (of 0). De som van al deze kwadraten gedeeld door het aantal punten geeft de MeanSquaredError (gemiddelde kwadraten som).
Verandering.
Onder de menu knop 
rechts boven staat de optie toon verandering die ervoor zorgt dat we gemakkelijk kunnen vaststellen in welke richting de MeanSquaredError verandert en met welke snelheid. De computer berekent snel het effect van een kleine verandering 
.Dit is een goede benadering van de afgeleide. Bij iedere knop staat de afgeleide. Belangrijk is of de afgeleide positief of negatief is in verband met dalen of stijgen van de MeanSquaredError.
Trainen netwerk
Je kunt ook het netwerk trainen. Dat wil zeggen in kleine stapjes steeds de meanSquaredError te verlagen. Voor deze training maakt het netwerk ook gebruik van de afgeleide. Je start het trainen met de knop Trainen netwerk. De computer doet dan 1000 keer een berekening. Ondertussen zie je de grafiek van het netwerk(licht blauw) langzaam de parabool(zwart) naderen. De meanSquaredError wordt steeds kleiner. Door nogmaals op deze knop te drukken worden weer 1000 keer de berekeningen uitgevoerd.
Opgaven Éen neuron
1) Eerst mag je zelf aan de knoppen draaien om te proberen de doelfunctie zo klein mogelijk te maken. Gebruik eventueel de buttons van -1 tot 1
2)a) Onder de options knop rechts boven staat de optie toon verandering die ervoor zorgt dat in welke richting de MeanSquaredError verandert en met welke snelheid. Dus een benadering van de afgeleide. 
.Bij iedere knop staat de (partiële) afgeleide. Probeer gebruik te maken van deze informatie. Als het netwerk automatisch leert, maakt het ook gebruik van de partiële afgeleiden,
b) Je kunt gemakkelijk controleren of de berekening correct verloopt. Gebruik daarvoor de 0.01 knop en je rekenmachine.
3) a) Automatisch. Je kunt ook de computer zelf laten rekenen met het trainen van het netwerk. Gebruik daarvoor de knop Trainen netwerk linksonder. De computer gaat dan uit van de positie waarin het netwerk staat. De computer biedt dan 1000 keer de 6 getallen aan het netwerk steeds in een random volgorde. Op grond van de fouten bij deze 6 getallen, worden de parameters van het netwerk een klein beetje aangepast.
b) Neem met behulp van de randomiseer-toets een totaal andere beginsituatie en kijk hoe het trainen dan gaat.
4) Voorspellen. Onder de menu-knop zit ook de mogelijkheid om te voorspellen.
i) Probeer eerst de waarde van de voorspelling met x = 3? en van x = 5? Vergelijk met de tabel.
ii) Onderzoek de voorspelling bij x = 20? Hoe groot is de error² ?
iii) Onderzoek x = -5?
iv) Wat is jouw verklaring voor de grote afwijkingen?
Twee neuronen
Met twee neuronen kun je de parabool nog beter benaderen. Je hebt dan de beschikking over twee lijnstukken die aan elkaar "vastzitten" In theorie kunnen die iedere positie krijgen met de 7 knoppen waaraan je kunt draaien, maar in de praktijk blijkt dat behoorlijk lastig te zijn.
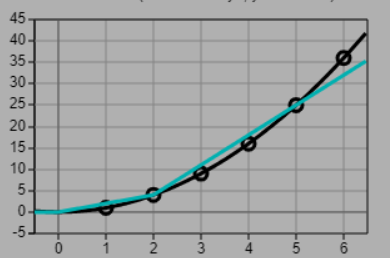
Je ziet de effecten op de grafiek. De weights bepalen de helling van de lijn. De bias de constante. Wat er getekend wordt in de grafieken kun je zien aan de titels van de grafieken. Je zult zien dat het best lastig is om een redelijke benadering van de parabool te vinden..
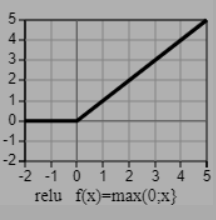
Daarnaast is er op twee plekken in het netwerk een activatie-functie. Als je geen activatie functie hebt, kun je alleen maar lineaire functies maken. De activatie-functie die we hier gebruiken is de relu-functie (Rectified Linear Units). De grafiek van de relu-functie staat links onder op het scherm. De definitie is f(x)=max(0,x). Dit is voor een computer een heel gemakkelijke functie. Als x>0 dan verandert er niets en anders wordt de functie 0. De plek waar de relu functie wordt toegepast is het blauwe vierkantje.
. .
Berekening van de MeanSquaredError
x-value |
y-value |
predicted |
error |
error² |
1 |
1 |
2.0 |
1.0 |
1.0 |
2 |
4 |
4.0 |
0.0 |
0.0 |
3 |
9 |
11.0 |
2.0 |
4.0 |
4 |
16 |
18.0 |
2.0 |
4.0 |
5 |
25 |
25.0 |
0.0 |
0.0 |
6 |
36 |
32.0 |
-4.0 |
16.0 |
MeanSquaredError = 4.2 Dit is het gemiddelde van de kwadraten in de laatste kolom. In deze situatie worden alleen de waarden in de punten 1,2 2, 3, 4 ,5 en 6 meegenomen.
wordt ook wel gemiddelde fout genoemd.
De learning rate geeft aan hoe groot de stappen mogen zijn die de computer neemt. Als de learningrate te klein is duurt het te lang. Als de stappen te groot zijn, kan het netweerk heel gauw bij getallen die buiten het bereik van de computer leggen.
Hulpmiddelen en vragen.
1) Eerst mag je zelf aan de knoppen draaien van de gewichten en van de bias om te proberen de doelfunctie zo klein mogelijk te maken.
2) Onder de options knop rechts boven staat de optie toon verandering die ervoor zorgt dat in welke richting de MeanSquaredError verandert en met welke snelheid. Dus een benadering van de afgeleide. 
.Bij iedere knop staat de (partiële) afgeleide. Probeer gebruik te maken van deze informatie. Als het netwerk automatisch leert, maakt het ook gebruik van de partiële afgeleiden,
3) Automatisch. Je kunt ook de computer zelf laten rekenen met het trainen van het netwerk. Gebruik daarvoor de knop Trainen netwerk linksonder. De computer biedt dan 1000 keer de 6 getallen aan het netwerk steeds in een random volgorde. Bij iedere aanbieding wordt het netwerk opnieuw uitgerekend. Regelmatig gaat het niet goed met zo'n klein netwerk en is het proces in een lokaal minimum beland waar het niet uitkomt. Soms kun je dat ook zien aan de grafieken. Die blijven ongveer op hun plaats en de kwadratensom wordt niet kleiner.Je moet dan gewoon opnieuw beginnen. Bij grotere netwerken heb je daar meestal geen last van.
4) Voorspellen. Onder de menu-knop zit ook de mogelijkheid om te voorspellen.
i) Probeer eerst de waarde van de voorspelling met x = 3? en van x = 5? Vergelijk met de tabel.
ii) Onderzoek de voorspelling bij x = 20? Hoe groot is de error² ?
iii) Onderzoek x = -5?
iv) Wat is jouw verklaring voor de grote afwijkingen?
5) Ook goed is om te zien dat er soms meerdere behoorlijk verschillende redelijke oplossingen zijn. Vergelijk met je buurman of probeer nog een keer
6) Kun je de volgende uitspraak bewijzen: Als je geen activatie functie hebt, kun je alleen maar lineaire functies maken met dit netwerk.
Meer punten en meer neuronen
Door de vanaf en de tot en met invoerveld aan te passen, verander je het gebied waar je de parabool wilt veranderen. Het netwerk benadert alleen de waarden bij de gehele getallen op de x-as.
Bij deze optie kun je zelf bepalen met welk netwerk je aan de slag gaat. Je kunt zowel het aantal neuronen per laag (layer) als het aantal lagen aanpassen.
Je kunt bij dit onderdeel niet zelf de parameters wijzigen. Je kunt alleen de hyper-parameters wijzigen, De computer doet dan zijn werk.
De app geeft ook het aantal parameters. Dit aantal kan behoorlijk oplopen.
1) Probeer maar netwerk te vinden met vanaf=-5 en tot en met is 5
2) Probeer maar een netwerk te vinden met vanaf=1 en tot en met =30?
3) Probeer eens met 200 neuronen in een laag?
4) Gaat 2) beter met twee lagen van 100 neuronen? Hoeveel parameters zijn er dan?
5) Gaat het ook met twee lagen en dan de eerste laag 20 neuronen en de tweede laag 10? Hoeveel parameters zijn er nu en is de kwaliteit echt veel slechter?