De wet van de grote aantallen is dat op de lange duur het waargenomen percentage successen gaat naar het verwachte percentage successen. Er zijn drie verschillende situaties gecreëerd in deze app.
Het drie deuren probleem, lootjes trekken en het tossen van een oneerlijke munt. Alle 3 de situaties laten zien, dat als je maar vaak genoeg simuleert, het waargenomen percentage gaat naar een vast percentage ( De zweetkans)
Het drie deuren probleem
Het drie deuren probleem is een zeer bekend kans probleem, dat vaak heftige reacties oproept. Moet je bij je keuze blijven of juist veranderen? Met deze app kunnen de leerlingen het zelf uitproberen. De app houdt de resultaten bij van de keuzes die gemaakt zijn. De grafiek van een aantal pogingen staat hieronder. Al na enkele tientallen pogingen is het grote verschil op succes bij de keuzes meestal zichtbaar. Als de gegevens van de hele klas getoond worden, zijn de resultaten overduidelijk.
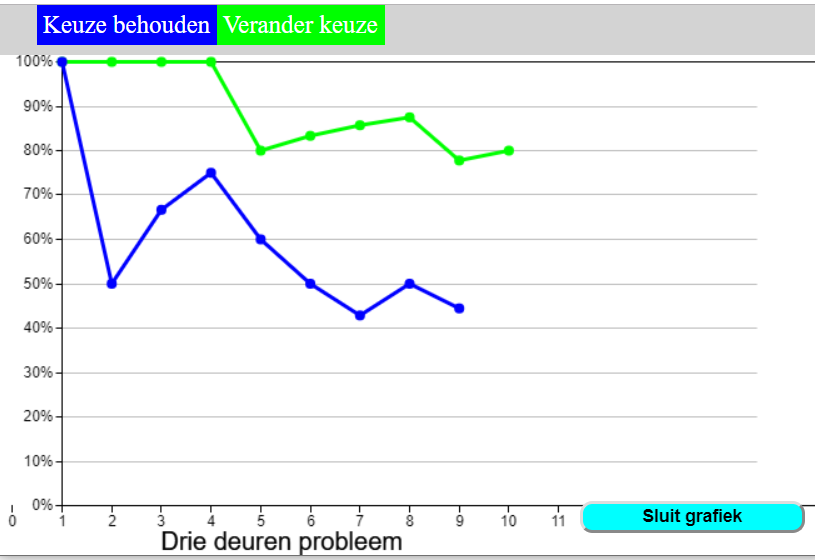
Verbinden met Internet met het drie deuren probleem.
Doordat de resultaten van al de leerlingen worden samen gevoegd, is er al snel een dataset die voldoende informatie geeft.
Een dataset heeft een code, dit is een getal met 6 cijfers. De dataset met code 123446 is al beschikbaar om te gebruiken. Wil je echter een eigen dataset hebben, dan moet je die aanmaken met de blauwe knop Internet op de startpagina van de app. Je kunt dan zelf een nieuwe dataset aanmaken met een eigen code en wachtwoord. Bij de start van de app moeten dan jouw leerlingen jouw code opgeven. De gegevens van de dataset blijven behouden op het internet zolang er iemand is ingelogd.
Lootjes trekken
In de tweede situatie gaat het over het lootjes trekken bij Sinterklaas en de kans dat iemand zichzelf trekt. Ook hier wordt eerst duidelijk gemaakt wat het probleem eigenlijk is. Wiskundig is het probleem al opgelost, maar vrijwel geen enkele leerling weet de oplossing. Door te simuleren kan de leerling het percentage te weten komen.
Gooien met (oneerlijke) munt
De derde situatie gaat over het tossen met een (oneerlijke) munt. Bij deze simulatie bestaat elk experiment uit een aantal worpen met een munt met een gegeven kans op kop. De simulatie laat het aantal kop en het aantal munt in een experiment zien. Je kunt het resultaat van een simulatie op verschillende manieren zien. In de vorm van een staafdiagram en in de vorm een grafiek met het percentage kop.
Trechter
In de grafiek rechtsonder wordt de relatieve frequentie van het aantal kop ten opzichte van het aantal worpen getoond. De grafiek is zo samengesteld dat na iedere worp de relatieve frequentie wordt berekend en als puntenrij getekend wordt. Hierdoor wordt de relatieve stabiliteit van de relatieve frequentie aanschouwelijk gemaakt, een voorbeeld van de wet van de grote aantallen. Anderzijds laat de grafiek ook zien dat er regelmatig uitzonderingen zijn (25, 50 en 100 zijn geen grote getallen). De trechter geeft het gebied aan waarbinnen de relatieve frequenties meestal liggen.
De resultaten van alle experimenten worden samengevat in een tabel rechtsonder op het scherm. Uiterst rechts staat een boxplot die de resultaten samenvat. Deze boxplot verschijnt pas na 5 experimenten.
Omvang
Hier geef je op uit hoeveel worpen een experiment bestaat.
Memory
Laat de resultaten zien van de laatste 10 experimenten
Raster
In heel licht grijs worden de mogelijke punten rijen getekend.