De wet van de kleine aantallen is "Kleine steekproeven leveren vaker een opvallend resultaat op dan grote steekproeven". De variatie in uitkomsten is veel groter.
In deze app worden twee situaties onderzocht. De eerste situatie is het percentage jongens dat geboren wordt in Nederlandse gemeentes. In de tweede situatie wordt gekeken naar het optreden van een zeldzame ziekte in de 3143 counties in de VS. Goede kennis van statistiek voorkomt foute conclusies.
Het percentage jongens dat per gemeente dat in Nederland in een jaar wordt geboren
Van alle gemeentes in Nederland worden het aantal geboortes en hoeveel daarvan jongens zijn bijgehouden. In de tabel links staan alle Nederlandse gemeentes op alfabetisch volgorde. Van elke gemeente is het aantal geboortes gegeven en het aantal jongetjes dat is geboren in die gemeente. De volgende kolom bevat het percentage jongens. Door op de kop van een kolom te klikken worden de gemeentes gesorteerd op die grootheid.
Deze gegevens worden in de grafiek aan de linkerkant getoond. Horizontaal staan het aantal geboortes en verticaal het percentage jongens in die gemeente. Het percentage mannelijke geboortes in heel Nederland is 51,10%. De x-as heeft een logaritmische schaal. Door met de muis over een rondje heen te gaan, verschijnen de bijbehorende gegevens van de desbetreffende gemeente.
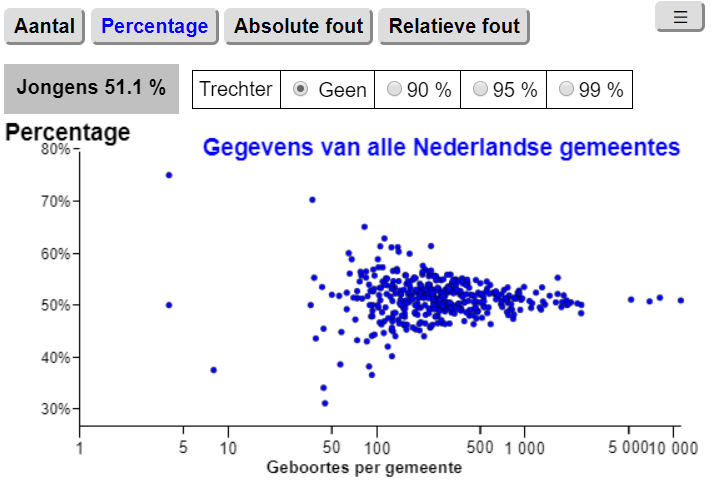
Duidelijk is te zien dat de spreiding van het percentage jongens groot is voor kleine gemeentes als Schiermonnikoog. Daartegenover is de spreiding in percentage jongens klein voor grote gemeentes. (Amsterdam (50,90%), Rotterdam (51,42%), Den Haag (50,72%)).
Er zijn vier verschillende soorten grafieken mogelijk:
•Aantal: Op de y-as staat het aantal geboortes. Dit is eigenlijk de onduidelijkste grafiek.
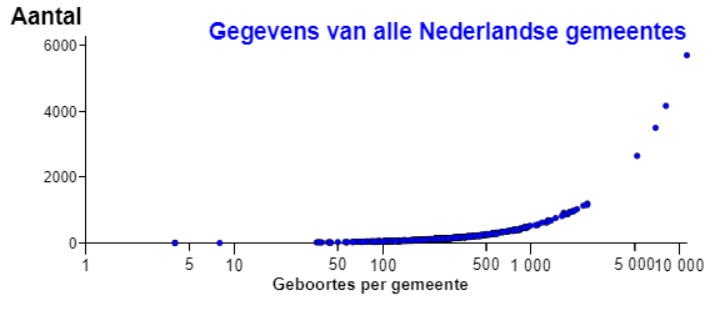
Dat de grafiek geen rechte lijn is, komt door de logaritmische x-as.
•Percentages: Op de y-as staat het percentage jongens. Op de grafiek is ook de trechter getekend met 95%. De trechter is het 95% voorspellingsinterval gebaseerd op de binomiale verdeling met p=51.1%
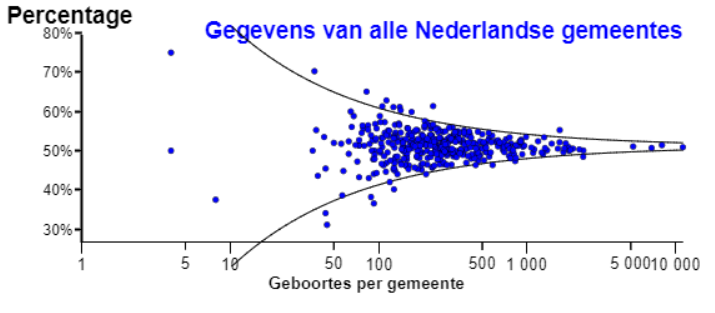
•Absolute fout. De absolute fout is het verschil tussen het aantal mannelijke geboortes en het verwachte aantal. De absolute fout is klein bij kleine gemeentes en soms groot bij grote gemeentes (Amsterdam (21,9), Rotterdam (26,7), Den Haag (62,1)).
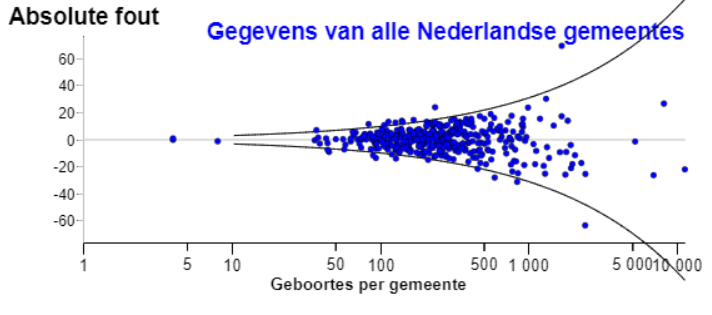
Ook hier vertekent de logaritmische as het beeld. Als de x-as lineair zou zijn, zou de trechter een wortel functie zijn.
•Relatieve fout. De relatieve fout is het verschil tussen het percentage mannelijke geboortes en het landelijke percentage mannelijke geboortes (51.1%)
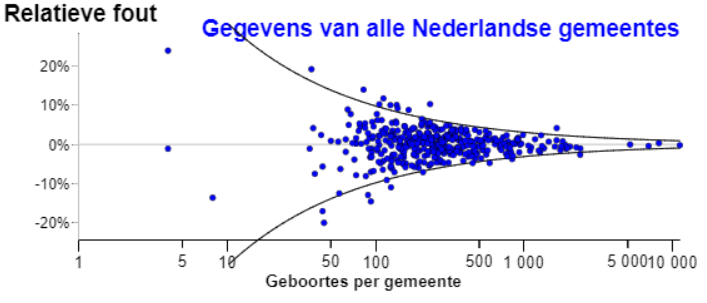
Deze grafiek lijkt erg op de grafiek van percentage. Alleen de y-as is nu verschoven.
Ander landen
Naast Nederland zijn ook grafieken van andere landen beschikbaar: België, Spanje, Nord-Carolina. Je ziet daar dezelfde verschijnselen als in Nederland,
Zeldzame ziektes (Nierkanker)
In de simulatie heeft iedere persoon in de 3143 counties van de VS dezelfde kans op nierkanker. Zie Daniel Kahneman "Thinking fast and slow". In onderstaande scherm is dat 0.0140
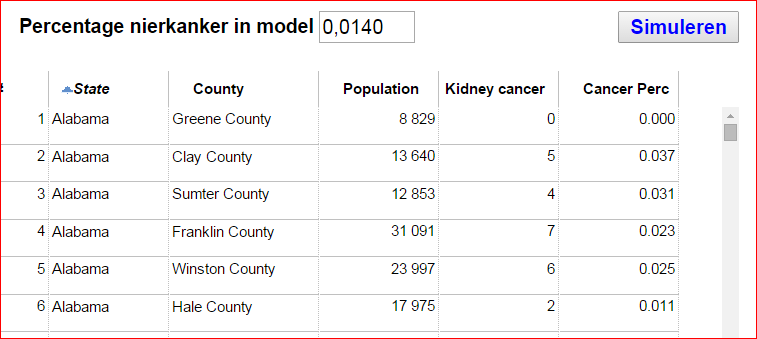
In deze tabel staan de gegevens van 3143 counties in de VS. De counties verschillen enorm qua populatieomvang.
De tweede kolom bevat de naam van de staat. De derde kolom bevat de naam van de county. De derde kolom de bevolkingsomvang. De vierde kolom zijn gesimuleerde aantallen. Bij de gesimuleerde aantallen is uitgegaan van een zeer kleine kans op nierkanker voor ieder persoon. Dit leidt tot de aantallen in kolom 4. Op grond van de omvang van de populatie worden vervolgens de percentages berekend. Door op de bovenste regel van de kolom te klikken wordt de tabel op grond van die kolom gesorteerd. Helaas zijn niet de echte aantal nierkanker patenten vanwege privacy redenen niet beschikbaar.
De uitvoer van deze simulatie wordt op verschillende manier gepresenteerd.:
Een tabel
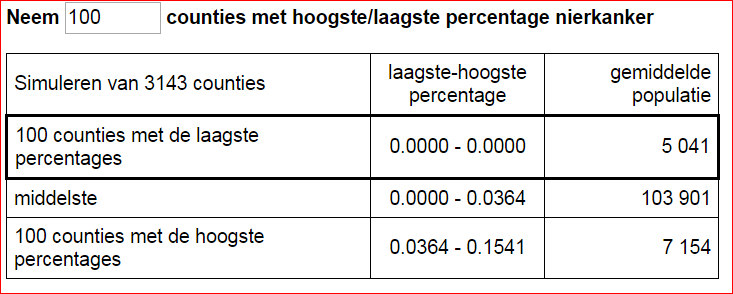
Uit de tabel is af te lezen dat de gemiddelde omvang van de populatie betrekkelijk klein is voor zowel de 100 counties met laagste percentage nierkanker als met hoogste percentage nierkanker. Dit verandert vrijwel niet als de simulatie op nieuw wordt uitgevoerd.
Meerdere soorten grafieken kunnen worden getoond.
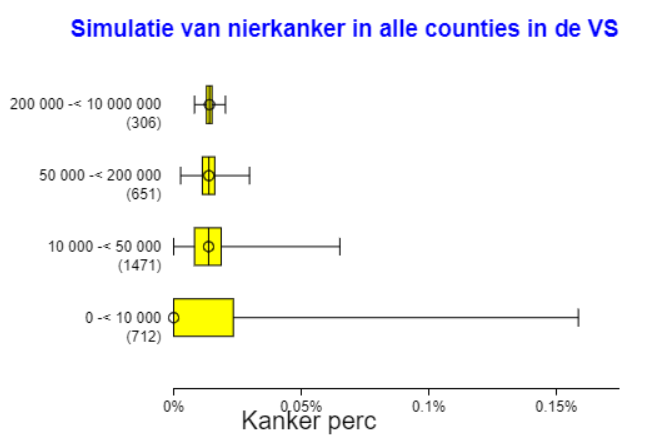
•De boxplot
Duidelijk is te zien dat de verschillen tussen de counties met een grote bevolkingsomvang de verschillen tussen de waargenomen percentage nierkanker heel klein is. Bij de counties met kleine populatieomvang is het daarentegen vrij groot.
•Aantal
De grafiek met op de x-as de omvang van de populatie en op de y-as het aantal nierkanker patenten. Duidelijk is dat het aantal nierkanker patiënten toeneemt naarmate de populatie groter is.
•Percentage
De grafiek met op de x-as de omvang van de populatie en op de y-as het percentage nierkanker patenten. Duidelijk is dat er bij kleine populaties counties zijn met een hoog percentage en met een laag percentage. De "vreemde " vorm van de grafiek ontstaat doordat het bij kleine populaties gaat om slechts een enkel kankergeval per county.
•Absolute fout
De grafiek met op de x-as de omvang van de populatie en op de y-as het verschil tussen het verwachte aantal en het waargenomen aantal. Duidelijk is de toename van de absolute fout bij grote populaties
•Relatieve fout
De grafiek met op de x-as de omvang van de populatie en op de y-as het verschil tussen het verwachte percentage en het waargenomen percentage. Duidelijk is de afname van de relatieve fout. Omdat er veel kleine counties zijn zonder een geval van nierkanker zijn er ook veel kleine counties met een lager dan verwacht percentage.