Dit voorbeeld komt uit hoofdstuk 17 van Daniel Kahneman Het feilbare brein. Wat iemand presteert hangt af van iemands capaciteiten en van het toeval. Aan de buitenkant kun je niet zien wat de rol van capaciteit en de rol van toeval is.
Met deze app kun je onderzoeken, hoe dit model vele alledaagse verschijnselen kan verklaren. De werkelijkheid wordt gemodelleerd door bij 300 mensen de uitkomst van twee testen te simuleren.
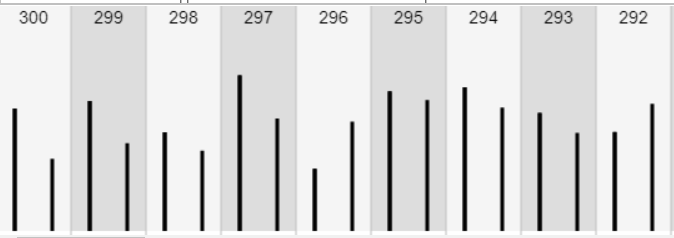
De eerste streep is de score op de eerste test en de tweede streep is de score op de tweede test. Je kunt deze grafiek manipuleren door te sorteren op de eerste test of te sorteren op de tweede test. De nummers zijn de nummers van de hokjes.
Alleen Toeval
Dit kun je instellen aan de bovenkant van het scherm. Als de prestatie alleen maar van het toeval zou afhangen en de test moet twee keer worden uitgevoerd zal er geen enkel verband zijn tussen de eerste poging en de tweede poging. De prestaties zijn normaal verdeeld met een spreiding van 10. Dat er geen verband is kun je zowel in de grafiek linksonder als in de tabel zien. Telkens als je een nieuwe steekproef neemt zul je zien dat de regressielijn bijna horizontaal loopt. In de tabel zul je zien als je de eerste groep in drieën verdeeld op grond van hun prestatie in de eerste test, de resultaten in de tweede test bijna niet verschillen voor de drie groepen.
Score=Talent + Geluk
Nu speelt talent wel een rol. Het talent is normaal verdeeld met een gemiddelde van 40 en een spreiding van 10. Je kunt de invloed hiervan op allerlei manieren zien. In de grafiek loopt de regressie lijn omhoog. Als je de proefpersonen op volgorde van de eerste poging zet, zul je zien dat bij de tweede poging de proefpersonen ongeveer dezelfde volgorde zal hebben.
Je ziet dat in de tabel de gemiddelde score van de laagste 100 weer de laagste is van de drie groepen. Ook geld dat de gemiddelde score van de van de hoogste 100 weer de hoogste is van de drie groepen.
Het verschijnsel Regressie naar het gemiddelde is dat van de groep die de eerste keer het laagste scoort het groepsgemiddelde omhoog gaat, terwijl van de groep die de eerste keer het hoogste scoort het groepsgemiddelde omlaag gaat.
Als verrassing dit geldt ook als je de rol van score1 en score 2 omdraait met ![]()
Hellinggrafiek
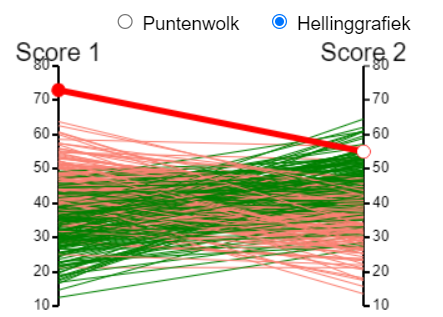
Een hellinggrafiek is zeer geschikt om stijgingen of dalingen te zien tussen de eerste en de tweede test. Ook hier wordt kleur gebruikt. Rood is afname en groen is toename.
Door de muis langs de assen te bewegen worden de resultaten van een andere persoon getoond.
De groene lijnen lopen meestal van linksonder naar boven, terwijl de rode lijnen meestal van linksboven naar rechtsonder lopen.
Beeld

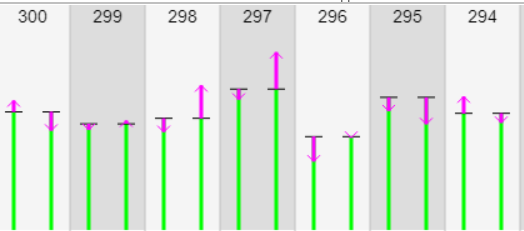
Als de optie Toon Opbouw aanstaat kun je de effecten van beide zien. De groene lijn staat voor het talent. De paarse pijl staat voor het geluk. De groene lijn bij iedere persoon is steeds even lang bij de eerste en tweede poging . De aanname is immers dat het talent niet wijzigt tussen de eerste en de tweede toets Er is goed te zien dat de gelukspijl een positief of een negatief effect kan hebben.
Als de optie Volgorde talent aan staat, verschijnt nog een extra rij getallen met een groene achtergrond. Deze extra rij is groen en geeft het rangnummer voor talent. In de figuur hieronder zijn de proefpersonen gesorteerd op de eerste test. Degene die het hoogste resultaat haalt op de eerste test is zeker niet degene met het meeste talent.
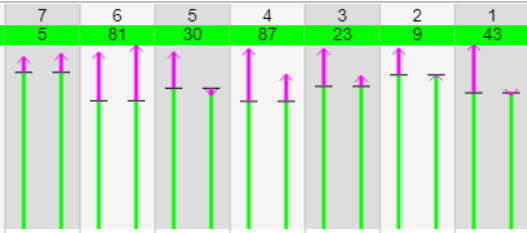
Een hellingplot is uitermate geschikt om toename van de eerste test naar de tweede test te zien.te zien. Ook is hier gebruik gemaakt van kleur. Rood is afname en groen is toename.
Door met de muis langs de assen te gaan wordt steeds de resultaten van een andere persoon getoond..
Ook met deze hellingplot kun je de regressie naar het gemiddelde laten zien.De groene lijnen gaan vooral van linksonder naar boven Terwijl de rode lijnen gaan vooral van rechtsboven naar beneden gaan.
Ten zeerste wordt aanbevolen hoofdstuk 17 van Kahneman te lezen.