De bootstrap voor het gemiddelde dient om een betrouwbaarheidsinterval voor gemiddelde of mediaan van de populatie te bepalen. De bootstrap voor het gemiddelde bestaat uit het vele malen doen van een steekproef uit de oorspronkelijke steekproef met terugleggen. Met deze app kun je onderzoeken wanneer bootstrap voor gemiddelde werkt. Is een steekproef van 5 groot genoeg? Werkt de methode ook goed bij extreme populaties?
Het scherm is verdeeld in drieën.
In het bovenste gedeelte van het scherm staan zowel de populatie als de steekproef. De populatie kun je aanpassen met je muis. Per experiment wordt een nieuwe steekproef getrokken die ook in het bovenste gedeelte van het scherm verschijnt. Ook de bootstrap steekproef wordt in het bovenste gedeelte van het scherm getoond. Als gekozen wordt voor het tempo stap voor stap bij het tempotool, wordt in de eerste stap alleen de steekproef getrokken uit de populatie en bij de volgende stap wordt de bootstrap steekproef getrokken uit die steekproef. Alle gekozen elementen van de steekproef krijgen een zwarte rand. De elementen uit de steekproef die vaker uitgekozen zijn krijgen een dikkere rand.
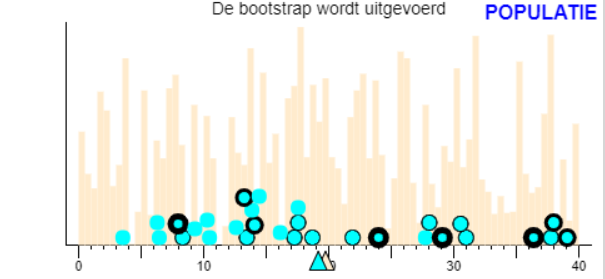
Bovenste gedeelte scherm
In het middelste gedeelte van het scherm staat de bootstrap verdeling, die ontstaan is door herhaalde steekproeven uit de oorspronkelijke steekproef. De linker en rechter grens van het 95% betrouwbaarheidsinterval worden bepaald door de gesimuleerde bootstrap verdeling. Bij een 95% betrouwbaarheidsinterval hebben 2.5% van de bootstrap steekproeven een lager gemiddelde dan de linker grens en 2.5% van de bootstrap steekproeven een hoger gemiddelde dan de rechter grens.

Middelste gedeelte scherm
In het onderste gedeelte van het scherm worden de gevonden betrouwbaarheidsintervallen getekend. Op grond van de originele steekproef kan met behulp van de t-verdeling de grenzen van het betrouwbaarheidsinterval bepaald worden. De resultaten van deze twee methoden om een betrouwbaarheidsinterval te bepalen kunnen hier vergeleken worden.
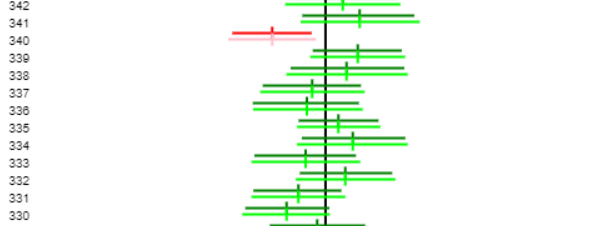
Het onderste scherm
Voor twee populaties
Met de bootstrap methode kunnen we ook een betrouwbaarheidsinterval vinden voor het verschil van het gemiddelde van twee populaties. De opmerkingen die hierboven gemaakt zijn voor een populatie gelden ook voor een populatie.
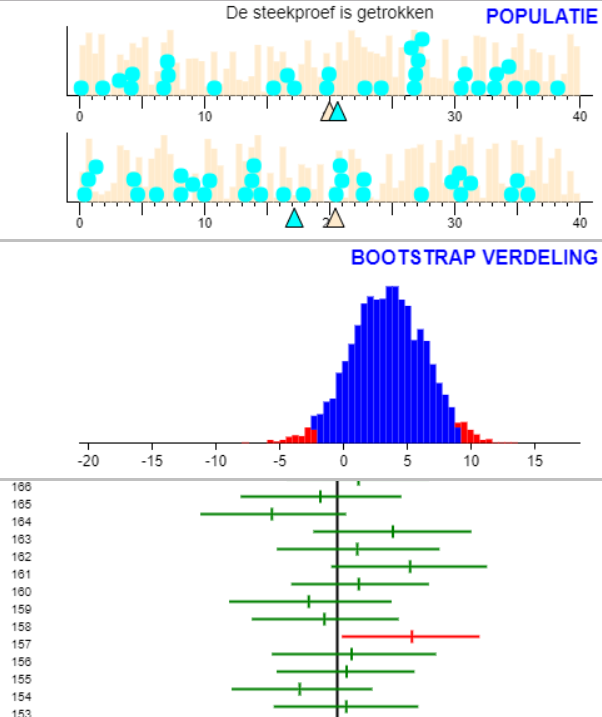
De drie gedeeltes van het scherm als je kiest voor twee populaties.