In deze app kan zowel gekozen worden voor de bootstrap als de randomisatie toets. De bootstrap methode kiest een groot aantal maal steekproeven uit de oorspronkelijke steekproeven. De randomisatie-toets gooit de twee groepen bij elkaar en trekt uit de gezamenlijke ballenbak een groot aantal trekkingen van de dezelfde omvang als de oorspronkelijke steekproeven.
De bootstrap

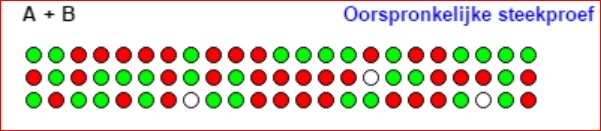
Bovenstaande plaatje laat zien hoe vaak ieder van de oorspronkelijke elementen getrokken zijn. Uit groep A wordt hetzelfde aantal getrokken als de oorspronkelijke omvang van groep A. Evenzo voor groep B.
Op grond van vele steekproeven die op een dergelijke manier zijn getrokken wordt een indruk gekregen van het betrouwbaarheidsinterval van het verschil tussen de proporties of het relatieve risico.
De randomisatie.
Bij de randomisatietoets is de vraag of het verschil tussen de proporties van de twee groepen verklaard kan worden door toeval. Bij de randomisatietoets wordt ervan uit gegaan dat er geen verschil is. De twee groepen worden bij elkaar gevoegd
Uit deze samengevoegde populatie worden zonder teruglegging weer twee groepen random gekozen. Door dit vaak te doen ontstaat een indruk van het verschil tussen de proporties van de twee steekproeven als er geen verschil was. Dit helpt bij de beslissing of er voldoende bewijs is dat er een echt verschil is tussen de proporties van de twee steekproeven.
In de app Steekproeven uit twee populaties, maar dan met verdeling proportie worden de vergelijkbare traditionele toetsen getoond.
.