Om informatie over een onbekende populatie te krijgen moet je steekproeven trekken.
De data die je met aselecte steekproeven verzamelt zijn de gegevens om centrummaten en spreidingsmaten van de populatie te schatten. Die schattingen hebben een mate van onbetrouwbaarheid ten gevolge van de toevalsvariatie in de steekproefdata. Die onbetrouwbaarheid kun je kleiner maken door grotere steekproeven te nemen. Maar in de praktijk betekent dat altijd ook een toename van de kosten.
Deze module geeft inzicht in het proces van het trekken van steekproeven en de samenvatting van de resultaten van die steekproeven in de steekproevenverdeling.
Je kunt het steekproefproces op verschillende manieren instellen en de animatie daarvan stapsgewijs of snel laten uitvoeren.
De populatie
Je kunt uit verschillende soorten populaties kiezen. De verdelingsgrafiek en de kentallen van de populatie worden weergegeven. Er zijn negen voor gedefinieerde verdelingen. Daarnaast kun je door slepen en vegen met de muis de laatste vijf verdelingen aan je eigen wensen aanpassen. Als je een populatie met de muis verandert passen de kentallen zich automatisch aan.
De populaties waar je de parameters van kunt wijzigen zijn: de normale verdeling, de uniform discrete verdeling, de uniform continue verdeling, de exponentiële verdeling.
Daarnaast is er een verdeling met proporties. Denk bijvoorbeeld aan een populatie met mensen die voor of die tegen zijn. Deze verdeling is aangeduid met de kleuren geel en paars. Als je toevalsgetallen gebruikt worden bij proporties vaak de waarden 0 en 1 gekozen. Bij proporties gaat het om discrete waarden, daarom zien de verdelingen er anders uit. Je kunt zowel de representatie als ballenbak als van verdeling zien.
De steekproef
Omvang van de steekproef kun je instellen.
Een stapsgewijze animatie laat zien hoe een steekproef tot stand komt (rode balletjes) en vervolgens hoe de “samenvatter” van die steekproef als één blauw balletje in de onderste grafiek verschijnt.
Standaard is ingesteld op het gemiddelde. Maar je kunt bij de steekproevenverdeling ook andere kentallen selecteren zoals mediaan, standaarddeviatie etc.
Een snelle simulatie geeft inzicht in de opbouw van de steekproevenverdeling.
De steekproevenverdeling
De steekproevenverdeling laat de verdeling van een kental van alle steekproeven zien. Je kunt zowel centrum als spreidingsmaten selecteren. Standaard is ingesteld op het gemiddelde en bij proporties op de proportie paars
De theoretische steekproevenverdeling is een limietverdeling, maar deze wordt al snel duidelijk met een redelijk aantal simulaties.
Verrassend is om te zien dat de steekproevenverdeling van het gemiddelde een normale verdeling wordt hoe vreemd de populatieverdeling er ook uitziet.
Via het onderste scherm kun je terugkijken op een "oude" trekking door op een bolletje te klikken. De bijbehorende trekking verschijnt dan in het middelste scherm
Bij een proportie-verdeling zie je dat de steekproevenverdeling een binomiale verdeling wordt.
Je kunt het resultaat vergelijken in de rubriek Verdelingen > Binomiale verdeling.
Centrum en Spreiding
Rechts boven kun je gemiddelde, mediaan en enkele spreidingsintervallen laten zien.
Daarmee kun je deze maten bij populatie en steekproef volgen gedurende de simulaties.
Bij de steekproevenverdeling moet deze optie met enig beleid worden gehanteerd.
Toetsen
Als aan de voorwaarden van de nulhypothese voldaan is, kan door een groot aantal keren de toets uit te voeren met behulp van de schuiven de grenzen van het kritieke gebied bepaald worden. Als niet aan de voorwaarde van de nulhypothese is voldaan kan onderzocht worden hoe de test zich gedraagt.
Voor de verdeling met proporties is een toets beschikbaar: de z-toets. Voor de binomiale toets zie de app Steekproeven uit ja-nee verdeling
Bij de z-toets moet de standaard deviatie van de populatie worden gegeven. De verdeling van de toetsingsgrootheid onder aanname van de nulhypothese wordt gegeven. In dit geval is dat de normale verdeling
Bij de t-toets is de aanname dat de populatie normaal verdeeld is. De verdeling van de toetsingsgrootheid onder de nulhypothese is dan de t-verdeling. Met dit onderdeel kan worden onderzocht hoe goed de t-toets presteert als niet aan de voorwaarde van de normale verdeling van de populatie is voldaan.
Met de Chi-kwadraat toets kan getoetst worden of de standaarddeviatie van de populatie een bepaalde waarde heeft. Deze toets is gevoelig voor afwijkingen van de normale verdeling.
Voorbeeldles ( Naar een idee van Jeroen Spandaw)
Neem de V-form verdeling als uitgangspunt.
Laat de leerlingen voorspellen hoe de steekproevenverdeling eruit ziet als de omvang van de steekproef 1 is?
Hoe als de de omvang van de steekproef 2 is?
Ga zo door met de omvang van de steekproef tot en met een omvang van 7
Laat daarna voorspellen hoe de steekproevenverdeling eruit ziet met met een omvang van 100.
De wet van de grote aantallen
In een statistische context zegt de wet van grote aantallen dat het (steekproef)gemiddelde van een aselecte steekproef uit een populatie, met hoge waarschijnlijkheid weinig verschilt van het populatiegemiddelde.
De onderstaande plaatjes laten zien wat dat betekent
Hoe de verdeling van de populatie ook is, steeds wordt de verdeling van de steekproefgemiddeldes vrijwel een rechte verticale lijn. Alle gemiddeldes zijn geconcentreerd rondom het populatie gemiddelde. Er zijn echter uitzonderingen.
In onderstaande grafieken is steeds gebruik gemaakt van steekproeven met omvang 6000. Let op dat je de steekproef als histogram laat tekenen, anders is de computer veel te lang bezig.
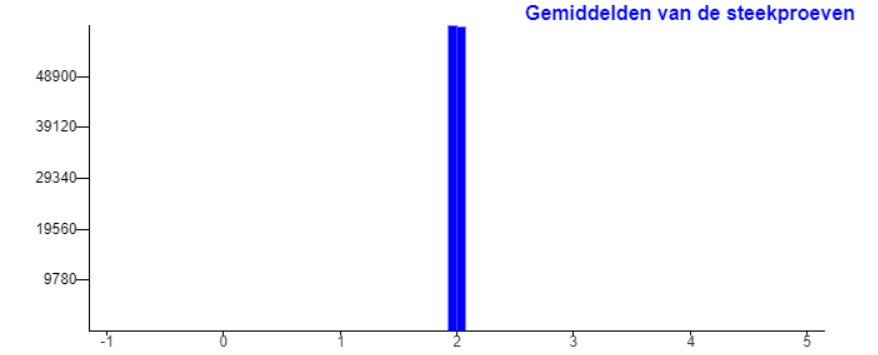
Verdeling van de gemiddeldes bij een steekproef met omvang 6000 waarbij de populatie een normale verdeling is met mu=2 en sigma=1
Opdracht. Doe hetzelfde bij de exponentiële verdeling, probeer het ook uit bij een eigen verdeling.
Opdracht . Voor de mediaan geldt niet altijd dat bij een zeer grote aselecte steekproef de mediaan van de steekproef weinig verschilt van de mediaan van de populatie. Laat dit zien met behulp van de app bij de discrete uniforme verdeling.
Conclusie: In de gevallen die wij onderzocht hebben, klopt de wet van de grote aantallen. Het opvallende is dat het gemiddelde van oneindig veel toevalsgrootheden iets heel deterministisch oplevert: Een constante. De kansmassa is in één punt gecentreerd. De stelling zegt echter niet hoe snel de convergentie gaat.
De centrale limietstelling
De Centrale limietstelling (central limit theorem) stelt dat de gemiddelden van steekproeven bij benadering normaal verdeeld zullen zijn als je steekproeven van voldoende omvang neemt uit een populatie, zelfs als die populatie niet normaal verdeeld is.
Ook deze stelling kun je met deze app onderzoeken.
Als je inzoomt op de gemiddelde van de steekproeven krijg je onderstaande grafiek.
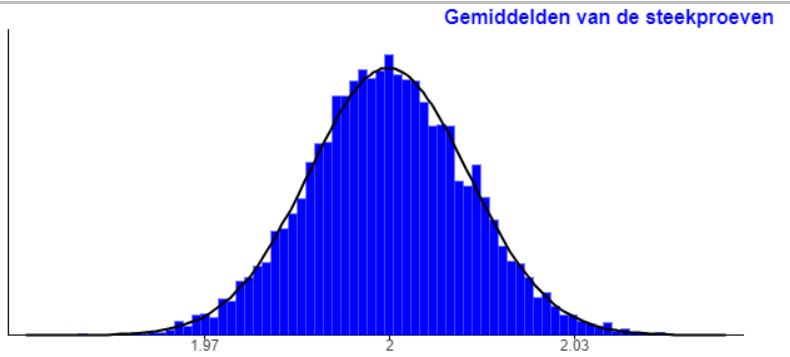
Ingezoomd op de "rechte lijn" krijg je de normale verdeling
Opdracht. Onderzoek ook bij andere verdelingen of het gemiddelde van de steekproefverdelingen naar de normale verdeling gaat.
Uitzondering.
Toch gaat de wet van de grote aantallen en de centrale limiet stelling niet altijd op. Namelijk bij de Cauchy verdeling gaat het mis. Neem een paar duizend steekproeven.
1) Wat gaat er mis bij de wet van de grote aantallen?
2) Wat gaat er mis bij centrale limiet stelling?
3) Wat zie je, als je ervoor kiest om hetzelfde beginpunt en eindpunt te nemen van de x-as als in de bovenste grafiek (Kies optie zelfde as)
4) Als je alle opties voor het domein uit zet krijg ik weer een rechte verticale streep. Toch gaat ook hier de wet van de grote aantallen niet op!! Kijk naar de numerieke gegevens aan de rechterkant van het scherm.
5) De Cauchy verdeling kan op eenvoudige wijze geconstrueerd worden. Zie onderstaande figuur met de eenheidscirkel waar in het midden van de cirkel een lamp brand. V
Extra. Als de extra eis gesteld wordt dat de variantie van de verdeling eindig is, dan geldt de centrale limiet stelling wel.