De populatie
Je kunt uit verschillende soorten populaties kiezen. De verdelingsgrafiek en de kentallen van de twee populaties worden weergegeven. Er zijn negen voor gedefinieerde verdelingen. Daarnaast kun je door slepen en vegen met de muis de laatste vijf verdelingen aan je eigen wensen aanpassen. Als je een populatie met de muis verandert passen de kentallen zich automatisch aan. Bij deze laatste vijf verdelingen kun je de tweede verdeling in zijn geheel verschuiven
De populaties waar je de parameters van kunt wijzigen zijn: de normale verdeling, de uniform continue verdeling, de exponent iele verdeling.
Daarnaast is er een verdeling met proporties. Denk bijvoorbeeld aan populaties mannen en vrouwen die voor of die tegen zijn. Deze verdeling is aangeduid met de kleuren paars en geel. Bij de proportie is de presentatie van ballenbak gekozen.
Met een knop aan de rechterkant worden de verdelingen van de twee populaties identiek.
De steekproef
De omvang van de steekproef in ieder van de twee populaties kun je instellen.
Een stapsgewijze animatie laat zien hoe een steekproef tot stand komt (rode balletjes) en vervolgens hoe de “samenvatter” van die steekproef als één blauw balletje in de onderste grafiek verschijnt.
Van de steekproef worden een aantal grootheden berekend: Gemiddelde, standaarddeviatie, scheefheid van iedere groep apart, Hieruit worden onder andere de t-test voor gelijke variantie, t-test voor ongelijke variantie, de Wilcoxon rangsom berekend.
Een snelle simulatie geeft inzicht in de opbouw van de steekproevenverdeling.
Via het onderste scherm kun je terugkijken op een "oude" trekking door op een bolletje te klikken. De bijbehorende trekking verschijnt dan in het middelste scherm.
Toetsen
Als het om proporties gaat kan gekozen worden tussen de z-toets of de chi-kwadraat toets. Bij alle andere populaties kan gekozen worden uit de t-toets bij gelijke varianties, de t-toets bij ongelijke varianties, de Wilcoxon rangtoets, de F-toets voor gelijke varianties en de test van Levene.
De z-toets voor verschil tussen twee proporties. De nulhypothese is dat de twee proporties gelijk zijn. De formule voor de z-toets is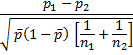 
waarbij p1 de waargenomen proportie in de eerste steekproef is en p2 de waargenomen proportie in de tweede steekproef en p het gewogen gemiddelde.
De chi-kwadraat toets voor onafhankelijkheid bij de kruistabel.
De rode cijfers aan de rechterkant van het middelste scherm zijn de verwachte aantallen bij onafhankelijkheid. Bij onafhankelijkheid is de nulverdeling bij benadering chi-kwadraat verdeeld met 1 vrijheidsgraad.
De t-toets bij gelijke varianties. H0: η1=η2
De verdeling van de toetsingsgrootheid als aan de nulhypothese is voldaan is een t-verdeling met n1+n2-2 vrijheidsgraden.
De t-toets is een hele robuuste toets. In het ideale geval zijn de populaties normaal verdeeld, Met deze app kan worden onderzocht wat het effect van afwijkingen is van de aannames.
De t-toets bij ongelijke varianties. H0: η1=η2.
Omdat het aantal vrijheidsgraden van de t-verdeling afhangt van de varianties, kan de nulverdeling niet worden getekend. Wel wordt bij iedere steekproef deze grootheid uitgerekend.
Wilcoxon rangsom toets H0 de medianen zijn gelijk.
Het is niet altijd redelijk om aan te nemen dat verdeling van de beide populaties normaal is. De rangsom toets van wilcoxon is dan een goed alternatief.
De F-toets s12/s22 . H0 : σ1=σ2
Deze test toets of de varianties van de twee populaties gelijk zijn.
De F-toets is geen robuuste toets. De eis van normaliteit van de populaties moet strikt worden genomen.
De toets van Levene. H0 σ1=σ2
Deze toets test ook of σ1=σ2 . Alleen deze toets van Levene is veel minder gevoelig voor afwijkingen van de normale verdeling van de populaties.